O numero de euler

Numero de Euler. Numero esquisito e misterioso, representado pela letra "e" e de valor aproximado de 2,71, é considerado um dos 5 numeros mais importantes da matemática, junto com 0, 1, π (a razão de uma circunferencia por seu diametro, pronuncia-se "pi") e ∞ (infinito).

Para a galera em geral, esse é o mais desconhecido desses, mas ele tem algumas propriedades extremamente curiosas.

1- Ele é a solução para o limite x->∞ (1+1/x)^x (^ representa potencia). Ou seja, 1+1 dividido por infinito, elevado a infinito, dá o numero de Euler.

Daí você pergunta, como resolveram isso?

Se você pega o x e substitui por um numero qualquer (no caso, 2), o valor será:

(1+1/2)^2 = 2,25

Nada a ver, né? Mas não dá pra se dizer que 2 está exatamente "proximo" do infinito.

Vamos ver com o 5

(1+1/5)^5= 2,48832

Está maior. Vamos tentar com 20.

(1+1/20)^20 = 2,653 297 705 144 420 133 945 430...

Esse numero (que embora pareça, não tem infinitos digitos) está bem mais proximo de "e", né? Isso porque 20 está bem mais proximo do infinito do que 2, por exemplo.

(1+1/100)^100 = 2,704 813 829 421 526 093 267 194...

Como podem ver, esse valor é muito proximo de "e", que vale cerca de 2,71, aproximadamente. Podemos perceber que quanto maior o numero colocado no lugar o x, mais devagar o valor da função cresce, ou seja, apesar de pudermos nos aproximar de "e" o quanto quisermos, jamais chegaremos nele (porque ele é o valor da função quando x = infinito)

(1+1/1.000.000)^1.000.000 = 2,718 280 469 319 376 883 819 799

Com x trocado por um milhão, o valor da função se aproxima ainda mais do numero de euler. Parei por aqui porque a calculadora do windows não estava aguentando calcular potencias por numeros muito maiores que esses, mas enfim, deu pra perceber a logica: quanto maior o valor de x, mais proximo de e ele chega, e se x fosse igual a infinito, o valor seria e:

(1+1/∞)^∞ = e = 2,718 281 828 459 045 235 360 287...

e é também um numero irracional e transcendente, ou seja, os digitos deles não seguem uma logica e não podem ser expressos por uma razão entre dois numeros inteiros. Trancendente porque "e" jamais vai ser o resultado de uma equação polinomial ou coisa do tipo, mas isso não importa, na verdade.

Ele também é o resultado da seguinte soma infinita abaixo:

1/0! + 1/1! + 1/2! + 1/3! + 1/4! ... assim, seguindo indenidamente.

Lembrando que "!" é o simbolo de "fatorial". Para lhe refrescar a memória:

0! = 1

1! = 1

2! = 2x1 = 2

3! = 3x2x1 = 6

4! = 4x3x2x1 = 24

5! = 5x4x3x2x1 = 120

E por aí vai. Lembrando que cada fração vai ficando exponencialmente menor, pois o divisor vai ficando cada vez maior:

Demonstrando:

1+1+0,5+0,16666...+0,04166666... + 0,00833333... e por aí vai. Essa soma indo do 1/0! até o 1/5! deu "2,716666666666666666666666666665", ou seja, tá ficando cada vez mais proxima de e, mas nunca vai chegar a ele, pois os valores das frações a serem somadas vão ficando menores a cada fator. Eventualmente, com infinitos termos, o valor seria "e".

Esse coiso abaixo também tende ao numero de Euler, mas não consegui entender direito que porra é essa:

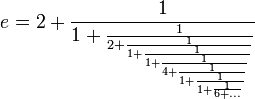
A função e^x também tem a interessante peculiaridade: sua derivada é ela própria. Ou seja, quando um economista, por exemplo, precisa tirar a derivada de alguma função financeira, ele pode colocar esta na força "e^x" para lhe poupar trabalho, usando logaritimos.

E bom, é isso aí.